Betting predictions skewed by [Mean, Median, Mode] cricket betting
Using a mean is the most common way to evaluate data for betting purposes, but is it the most useful? Median and Mode also provide a more suitable alternative, so knowing them is important to the effective betting method.

Bettors ‘Mean’ problems
Thanks to its simplicity, many sports bettors use the mean for statistically quantifying an output. But who will conscious of its flaws?
For example, when betting for a football match on the Total Goals market, bettors may think that by measuring the mean of goals scored in previous games, it provides a reliable gage of the number of goals anticipated in a future match. But is the mean calculation likely to fit?
As a reference, let us compare the number of goals scored in the Premier League in the 2013/14 season against La Liga. For each league, the average goals scored per game are 2.77 and 2.75, respectively. It could lead bettors to believe that in La Liga, scoring less than 2.5 goals, are more common than in the Premier League. Though that is not true, 48.40% of Premier League games go under 2.5 goals compare to 47.30% in La Liga.
The chart below showed that it is noticeable that although the number distribution is identical, the Premier League highest number of goals scored is 2 goals per match compared to 3 goals per match in La Liga. The mean has covered the truth.
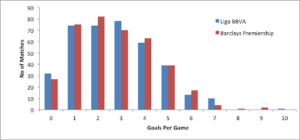
Even if the mean gives an overall view, the shape of the number does not account for this.
One example of the risks of mean tests is to use them to determine handicaps for minnow nations in international soccer, who are perceived to be the person blamed for each qualification drive. Yet, are they really just as poor as they seem? While the mean of nations scored per game may result in large numbers, this figure may have been severely skewed by less frequent but heavy losses, leading bettors expectation to overestimate the amount of goals.
We discuss alternatives to the mean, median, and mode, by using three groups of numbers to illustrate two cases where the average may not be satisfactory.
Consider the number of groups below, and each has a mean of five.
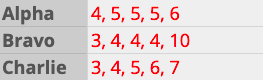
1st Situation: Getting outliers at the higher/lower end.
Even though all three groups have the same total(25) and mean(5), but their distribution is very different.
Alpha can defined as being symmetrically distributed; on each end of the mean, there is one number, while 4 is below the mean, and 6 is above.
The mean is best to use when dealing with a symmetric distribution-a situation in which the values of variables arise on both ends of the average at equal frequencies, and the mean is in the center of the value set.
In contrast, Bravo has 4 numbers underneath the average and only one greater. This may be defined as a skewed distribution.
The usage of massive data set, bettors can take a look at the suitability of the mean by the use of different measures along with the mode or median.
The median is the value that, when placed in ascending or descending order, is in the center of a distribution. There are 5 and 4 in Alpha and Bravo, respectively. The most common value is the mode, which is also 5 and 4, respectively.
A symmetric distribution has to have comparable mathematics suggest, median, and mode. The distinction between the arithmetic mean and the latter two in Bravo indicates that this is a skewed distribution, and consequently, the average isn’t a really perfect measure.
2nd Situation: Distinctive Range
Two groups can both be distributed symmetrically but not distributed evenly. For instance, Alpha and Charlie is also symmetrically distributed, since it has identical numbers below and above the average, and the deviation from the mean is equivalent on both ends.
And while both reasonably represented by an average of five, this average is a better measure for set A, since more numbers are closer to the arithmetic mean. The disparity between the two groups falls in dispersion. So we have to calculate the distribution.
The bettors should measure the range and the standard deviation for this reason. The variety and the difference from the maximum to the minimum value because it is simple to measure. Standard deviation, on the other hand, is more difficult. In simple terms, and for this article’s significance, it calculates the variance from the average in a collection of data.
Alpha and Charlie respectively have varieties of two and four, while their standard deviation is 0.71 and 1.58, respectively. We have more indication that there is more variation within the latter category as both measurements are higher for Charlie.
Conclusion
By recognizing the mean drawbacks, skew distributions, and various dispersion metrics-bettors would be better prepared to determine their suitability as a predictive measure. Though not a detailed inquiry into the appropriateness of using the mean, this should be adequate to urge caution and suggest other steps.





